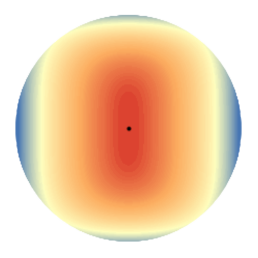
Ensembles are a straightforward, remarkably effective method for improving the accuracy, calibration, and robustness of neural networks on classification tasks. Yet, the reasons underlying their success remain an active area of research. Building upon (Pfau, 2013), we turn to the bias-variance decomposition of Bregman divergences in order to gain insight into the behavior of ensembles under classification losses. Introducing a dual reparameterization of the bias-variance decomposition, we first derive generalized laws of total expectation and variance, then discuss how bias and variance terms can be estimated empirically. Next, we show that the dual reparameterization naturally introduces a way of constructing ensembles which reduces the variance and leaves the bias unchanged. Conversely, we show that ensembles that directly average model outputs can arbitrarily increase or decrease the bias. Empirically, we see that such ensembles of neural networks may reduce the bias. We conclude with an empirical analysis of ensembles over neural network architecture hyperparameters, revealing that these techniques allow for more efficient bias reduction than standard ensembles.

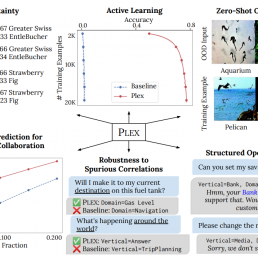
A recent trend in artificial intelligence is the use of pretrained models for language and vision tasks, which have achieved extraordinary performance but also puzzling failures. Probing these models’ abilities in diverse ways is therefore critical to the field. In this paper, we explore the reliability of models, where we define a reliable model as one that not only achieves strong predictive performance but also performs well consistently over many decision-making tasks involving uncertainty (e.g., selective prediction, open set recognition), robust generalization (e.g., accuracy and proper scoring rules such as log-likelihood on in- and out-of-distribution datasets), and adaptation (e.g., active learning, few-shot uncertainty). We devise 10 types of tasks over 40 datasets in order to evaluate different aspects of reliability on both vision and language domains. To improve reliability, we developed ViT-Plex and T5-Plex, pretrained large model extensions for vision and language modalities, respectively. Plex greatly improves the state-of-the-art across reliability tasks, and simplifies the traditional protocol as it improves the out-of-the-box performance and does not require designing scores or tuning the model for each task. We demonstrate scaling effects over model sizes up to 1B parameters and pretraining dataset sizes up to 4B examples. We also demonstrate Plex’s capabilities on challenging tasks including zero-shot open set recognition, active learning, and uncertainty in conversational language understanding.

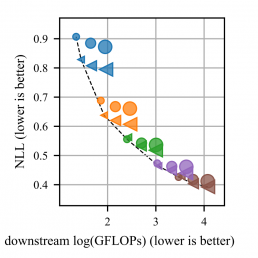
Machine learning models based on the aggregated outputs of submodels, either at the activation or prediction levels, lead to strong performance. We study the interplay of two popular classes of such models: ensembles of neural networks and sparse mixture of experts (sparse MoEs). First, we show that these two approaches have complementary features whose combination is beneficial. Then, we present partitioned batch ensembles, an efficient ensemble of sparse MoEs that takes the best of both classes of models. Extensive experiments on fine-tuned vision transformers demonstrate the accuracy, log-likelihood, few-shot learning, robustness, and uncertainty calibration improvements of our approach over several challenging baselines. Partitioned batch ensembles not only scale to models with up to 2.7B parameters, but also provide larger performance gains for larger models.

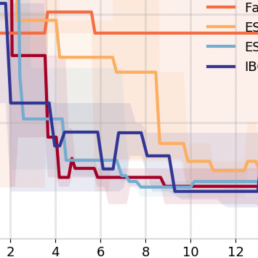
Many contemporary machine learning models require extensive tuning of hyperparameters to perform well. A variety of methods, such as Bayesian optimization, have been developed to automate and expedite this process. However, tuning remains costly as it typically requires repeatedly fully training models. To address this issue, Bayesian optimization has been extended to use cheap, partially trained models to extrapolate to expensive complete models. This approach enlarges the set of explored hyperparameters, but including many low-fidelity observations adds to the intrinsic randomness of the procedure and makes extrapolation challenging. We propose to accelerate tuning of neural networks in a robust way by taking into account the relative amount of information contributed by each training example. To do so, we leverage importance sampling (IS); this significantly increases the quality of the function evaluations, but also their runtime, and so must be done carefully. Casting hyperparameter search as a multi-task Bayesian optimization problem over both hyperparameters and IS design achieves the best of both worlds. By learning a parameterization of IS that tradeso↵ evaluation complexity and quality, our method improves upon validation error, in the average and worst-case, while using higher fidelity observations with less data. We show that this results in more reliable performance of our method in less wall-clock time across a variety of datasets and neural architectures.

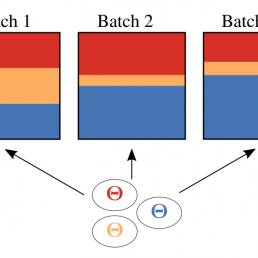
The use of black-box optimization for the design of new biological sequences is an emerging research area with potentially revolutionary impact. The cost and latency of wet-lab experiments requires methods that find good sequences in few experimental rounds of large batches of sequences–a setting that off-the-shelf black-box optimization methods are ill-equipped to handle. We find that the performance of existing methods varies drastically across optimization tasks, posing a significant obstacle to real-world applications. To improve robustness, we propose Population-Based Black-Box Optimization (P3BO), which generates batches of sequences by sampling from an ensemble of methods. The number of sequences sampled from any method is proportional to the quality of sequences it previously proposed, allowing P3BO to combine the strengths of individual methods while hedging against their innate brittleness. Adapting the hyper-parameters of each of the methods online using evolutionary optimization further improves performance. Through extensive experiments on in-silico optimization tasks, we show that P3BO outperforms any single method in its population, proposing higher quality sequences as well as more diverse batches. As such, P3BO and Adaptive-P3BO are a crucial step towards deploying ML to real-world sequence design.

This thesis establishes negative dependence as a powerful and computationally efficient framework to analyze machine learning problems that require a theoretical model of diversification. Examples of such problems include experimental design and model compression: subset-selection problems that require carefully balancing the quality of each selected element with the diversity of the subset as a whole. Negative dependence, which models the behavior of “repelling” random variables, provides a rich mathematical framework for the analysis of such problems.

The first part of this thesis develops scalable sampling and learning algorithms for determinantal point processes (DPPs), popular negatively dependent measures with many applications to machine learning. For scalable sampling, we introduce a theoretically-motivated generative deep neural network for DPP-like samples over arbitrary ground sets. To address the learning problem, we show that algorithms for maximum likelihood estimation (MLE) for DPPs are drastically sped up with Kronecker kernels, and that MLE can be further enriched by negative samples.

The second part of this thesis leverages negative dependence for core problems in machine learning. We begin by deriving a generalized form of volume sampling (GVS) based on elementary symmetric polynomials, and prove that the induced measures exhibit strong negative dependence properties. We then show that classical forms of optimal experimental design can be cast as optimization problems based on GVS, for which we derive randomized and greedy algorithms to obtain the associated designs. Finally, we introduce exponentiated strongly Rayleigh measures, which allow for simple tuning of the strength of repulsive forces between similar items while still enjoying fast sampling algorithms. The great flexibility of exponentiated strongly Rayleigh measures makes them an ideal tool for machine learning problems that benefit from negative dependence theory.

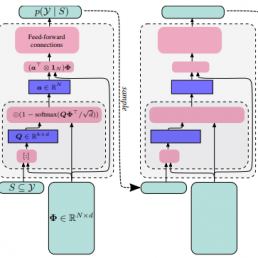
Determinantal Point Processes (DPPs) provide an elegant and versatile way to sample sets of items that balance the point-wise quality with the set-wise diversity of selected items. For this reason, they have gained prominence in many machine learning applications that rely on subset selection. However, sampling from a DPP over a ground set of size N is a costly operation, requiring in general an O(N^3) preprocessing cost and an O(Nk^3) sampling cost for subsets of size k. We approach this problem by introducing DPPNets: generative deep models that produce DPP-like samples for arbitrary ground sets. We develop an inhibitive attention mechanism based on transformer networks that captures a notion of dissimilarity between feature vectors. We show theoretically that such an approximation is sensible as it maintains the guarantees of inhibition or dissimilarity that makes DPPs so powerful and unique. Empirically, we demonstrate that samples from our model receive high likelihood under the more expensive DPP alternative.

The availability of large amounts of time series data, paired with the performance of deep-learning algorithms on a broad class of problems, has recently led to significant interest in the use of sequence-to-sequence models for time series forecasting. We provide the first theoretical analysis of this time series forecasting framework. We include a comparison of sequence-to-sequence modeling to classical time series models, and as such our theory can serve as a quantitative guide for practitioners choosing between different modeling methodologies.

Determinantal Point Processes (DPPs) have attracted significant interest from the machine-learning community due to their ability to elegantly and tractably model the delicate balance between quality and diversity of sets. We consider learning DPPs from data, a key task for DPPs; for this task, we introduce a novel optimization problem, Contrastive Estimation (CE), which encodes information about “negative” samples into the basic learning model. CE is grounded in the successful use of negative information in machine-vision and language modeling. Depending on the chosen negative distribution (which may be static or evolve during optimization), CE assumes two different forms, which we analyze theoretically and experimentally. We evaluate our new model on real-world datasets; on a challenging dataset, CE learning delivers a considerable improvement in predictive performance over a DPP learned without using contrastive information.

Strongly Rayleigh (SR) measures are discrete probability distributions over the subsets of a ground set. They enjoy strong negative dependence properties, as a result of which they assign higher probability to subsets of diverse elements. We introduce in this paper Exponentiated Strongly Rayleigh (ESR) measures, which sharpen (or smoothen) the negative dependence property of SR measures via a single parameter (the exponent) that can intuitively understood as an inverse temperature. We develop efficient MCMC procedures for approximate sampling from ESRs, and obtain explicit mixing time bounds for two concrete instances: exponentiated versions of Determinantal Point Processes and Dual Volume Sampling. We illustrate some of the potential of ESRs, by applying them to a few machine learning tasks; empirical results confirm that beyond their theoretical appeal, ESR-based models hold significant promise for these tasks.

Determinantal point processes (DPPs) are well-suited to recommender systems where the goal is to generate collections of diverse, high-quality items. In the existing literature this is usually formulated as finding the mode of the DPP (the so-called MAP set). However, the MAP objective inherently assumes that the DPP models “optimal” recommendation sets, and yet obtaining such a DPP is nontrivial when there is no ready source of example optimal sets. In this paper we advocate an alternative framework for applying DPPs to recommender systems. Our approach assumes that the DPP simply models user engagements with recommended items, which is more consistent with how DPPs for recommender systems are typically trained. With this assumption, we are able to formulate a metric that measures the expected number of items that a user will engage with. We formalize this optimization of this metric as the Maximum Induced Cardinality (MIC) problem. Although the MIC objective is not submodular, we show that it can be approximated by a submodular function, and that empirically it is well-optimized by a greedy algorithm.

We revisit the classical problem of optimal experimental design (OED) under a new mathematical model grounded in a geometric motivation. Specifically, we introduce models based on elementary symmetric polynomials; these polynomials capture “partial volumes” and offer a graded interpolation between the widely used A-optimal and D-optimal design models, obtaining each of them as special cases. We analyze properties of our models, and derive both greedy and convex-relaxation algorithms for computing the associated designs. Our analysis establishes approximation guarantees on these algorithms, while our empirical results substantiate our claims and demonstrate a curious phenomenon concerning our greedy algorithm. Finally, as a byproduct, we obtain new results on the theory of elementary symmetric polynomials that may be of independent interest.

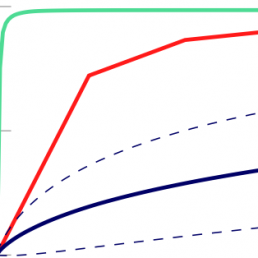
Determinantal Point Processes (DPPs) are probabilistic models over all subsets a ground set of N items. They have recently gained prominence in several applications that rely on diverse subsets. However, their applicability to large problems is still limited due to O(N^3) complexity of core tasks such as sampling and learning. We enable efficient sampling and learning for DPPs by introducing KronDPP, a DPP model whose kernel matrix decomposes as a tensor product of multiple smaller kernel matrices. This decomposition immediately enables fast exact sampling. But contrary to what one may expect, leveraging the Kronecker product structure for speeding up DPP learning turns out to be more difficult. We overcome this challenge, and derive batch and stochastic optimization algorithms for efficiently learning the parameters of a KronDPP.

As machine-learning techniques continue to require more data and become increasingly memory-heavy, being able to choose a subset of relevant, high-quality and diverse elements among large amounts of redundant or noisy data and parameters has become an important concern. Here, we approach this problem using Determinantal Point Processes (DPPs), probabilistic models that provide an intuitive and powerful way of balancing quality and diversity in sets of items. We introduce a novel, fixed-point algorithm for estimating the maximum likelihood parameters of a DPP, provide proof of convergence and discuss generalizations of this technique. We then apply DPPs to the difficult problem of detecting and eliminating redundancy in fully-connected layers of neural networks. By placing a DPP over a layer, we are able to sample a subset of neurons that perform non-overlapping computations and merge all other neurons of the layer into the previous diverse subset. This allows us to significantly reduce the size of the neural network while simultaneously maintaining a good performance.

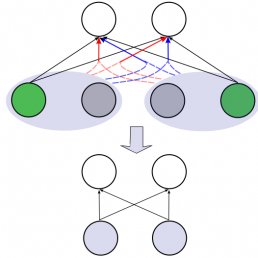
We introduce Divnet, a flexible technique for learning networks with diverse neurons. Divnet models neuronal diversity by placing a Determinantal Point Process (DPP) over neurons in a given layer. It uses this DPP to select a subset of diverse neurons and subsequently fuses the redundant neurons into the selected ones. Compared with previous approaches, Divnet offers a more principled, flexible technique for capturing neuronal diversity and thus implicitly enforcing regularization. This enables effective auto-tuning of network architecture and leads to smaller network sizes without hurting performance. Moreover, through its focus on diversity and neuron fusing, Divnet remains compatible with other procedures that seek to reduce memory footprints of networks. We present experimental results to corroborate our claims: for pruning neural networks, Divnet is seen to be notably superior to competing approaches.

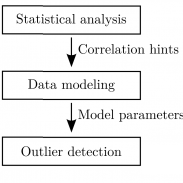
Abstract—Rapidly developing areas of information technology are generating massive amounts of data. Human errors, sensor failures, and other unforeseen circumstances unfortunately tend to undermine the quality and consistency of these datasets by introducing outliers – data points that exhibit surprising behavior when compared to the rest of the data. Characterizing, locating, and in some cases eliminating these outliers offers interesting insight about the data under scrutiny and reinforces the confidence that one may have in conclusions drawn from otherwise noisy datasets. In this paper, we describe a tuple expansion procedure which reconstructs rich information from semantically poor SQL data types such as strings, integers, and floating point numbers. We then use this procedure as the foundation of a new user-guided outlier detection framework, dBoost, which relies on inference and statistical modeling of heterogeneous data to flag suspicious fields in database tuples. We show that this novel approach achieves good classification performance, both in traditional numerical datasets and in highly non-numerical contexts such as mostly textual datasets. Our implementation is publicly available, under version 3 of the GNU General Public License.

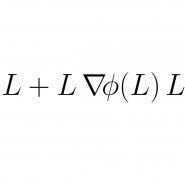
Determinantal point processes (DPPs) offer an elegant tool for encoding probabilities over subsets of a ground set. Discrete DPPs are parametrized by a positive semidefinite matrix (called the DPP kernel), and estimating this kernel is key to learning DPPs from observed data. We consider the task of learning the DPP kernel, and develop for it a surprisingly simple yet effective new algorithm. Our algorithm offers the following benefits over previous approaches: (a) it is much simpler; (b) it yields equally good and sometimes even better local maxima; and (c) it runs an order of magnitude faster on large problems. We present experimental results on both real and simulated data to illustrate the numerical performance of our technique.