SR measures
Publication Types:

It is often desirable for recommender systems and other information retrieval applications to provide diverse results, and determinantal point processes (DPPs) have become a popular way to capture the trade-off between the quality of individual results and the diversity of the overall set. However, computational concerns limit the usefulness of DPPs in practice. Sampling from a DPP is inherently expensive: if the underlying collection contains N items, then generating each DPP sample requires O(N) time following a one-time preprocessing phase. Additionally, results often need to be personalized to a user, but standard approaches to personalization invalidate the preprocessing, making personalized samples especially expensive. In this work we address both of these shortcomings. First, we propose a new algorithm for generating DPP samples in O(log N) time following a slightly more expensive preprocessing phase. We then extend the algorithm to support arbitrary query-time feature weights, allowing us to generate samples customized to individual users while still retaining logarithmic runtime. Experiments show that our approach runs over 300 times faster than traditional DPP sampling on collections of 100,000 items for samples of size 10.
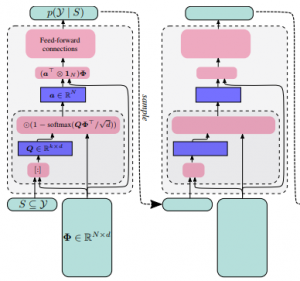
DppNet: Approximating Determinantal Point Processes with Deep Networks
Determinantal Point Processes (DPPs) provide an elegant and versatile way to sample sets of items that balance the point-wise quality with the set-wise diversity of selected items. For this reason, they have gained prominence in many machine learning applications that rely on subset selection. However, sampling from a DPP over a ground set of size N is a costly operation, requiring in general an O(N^3) preprocessing cost and an O(Nk^3) sampling cost for subsets of size k. We approach this problem by introducing DPPNets: generative deep models that produce DPP-like samples for arbitrary ground sets. We develop an inhibitive attention mechanism based on transformer networks that captures a notion of dissimilarity between feature vectors. We show theoretically that such an approximation is sensible as it maintains the guarantees of inhibition or dissimilarity that makes DPPs so powerful and unique. Empirically, we demonstrate that samples from our model receive high likelihood under the more expensive DPP alternative.
Learning Determinantal Point Processes by Sampling Inferred Negatives
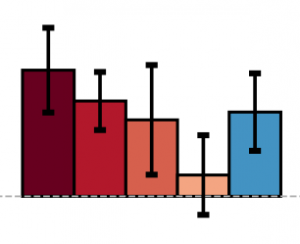
Determinantal Point Processes (DPPs) have attracted significant interest from the machine-learning community due to their ability to elegantly and tractably model the delicate balance between quality and diversity of sets. We consider learning DPPs from data, a key task for DPPs; for this task, we introduce a novel optimization problem, Contrastive Estimation (CE), which encodes information about “negative” samples into the basic learning model. CE is grounded in the successful use of negative information in machine-vision and language modeling. Depending on the chosen negative distribution (which may be static or evolve during optimization), CE assumes two different forms, which we analyze theoretically and experimentally. We evaluate our new model on real-world datasets; on a challenging dataset, CE learning delivers a considerable improvement in predictive performance over a DPP learned without using contrastive information.
Exponentiated Strongly Rayleigh Distributions
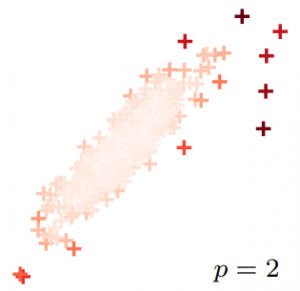
Strongly Rayleigh (SR) measures are discrete probability distributions over the subsets of a ground set. They enjoy strong negative dependence properties, as a result of which they assign higher probability to subsets of diverse elements. We introduce in this paper Exponentiated Strongly Rayleigh (ESR) measures, which sharpen (or smoothen) the negative dependence property of SR measures via a single parameter (the exponent) that can intuitively understood as an inverse temperature. We develop efficient MCMC procedures for approximate sampling from ESRs, and obtain explicit mixing time bounds for two concrete instances: exponentiated versions of Determinantal Point Processes and Dual Volume Sampling. We illustrate some of the potential of ESRs, by applying them to a few machine learning tasks; empirical results confirm that beyond their theoretical appeal, ESR-based models hold significant promise for these tasks.
Elementary Symmetric Polynomials for Optimal Experimental Design
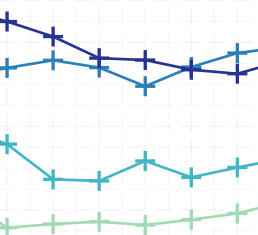
We revisit the classical problem of optimal experimental design (OED) under a new mathematical model grounded in a geometric motivation. Specifically, we introduce models based on elementary symmetric polynomials; these polynomials capture “partial volumes” and offer a graded interpolation between the widely used A-optimal and D-optimal design models, obtaining each of them as special cases. We analyze properties of our models, and derive both greedy and convex-relaxation algorithms for computing the associated designs. Our analysis establishes approximation guarantees on these algorithms, while our empirical results substantiate our claims and demonstrate a curious phenomenon concerning our greedy algorithm. Finally, as a byproduct, we obtain new results on the theory of elementary symmetric polynomials that may be of independent interest.

Learning and enforcing diversity with Determinantal Point Processes
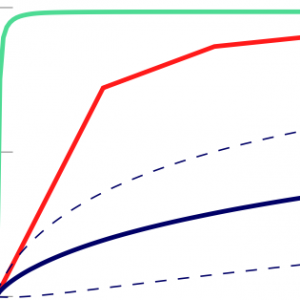
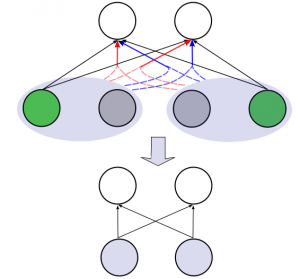
As machine-learning techniques continue to require more data and become increasingly memory-heavy, being able to choose a subset of relevant, high-quality and diverse elements among large amounts of redundant or noisy data and parameters has become an important concern. Here, we approach this problem using Determinantal Point Processes (DPPs), probabilistic models that provide an intuitive and powerful way of balancing quality and diversity in sets of items. We introduce a novel, fixed-point algorithm for estimating the maximum likelihood parameters of a DPP, provide proof of convergence and discuss generalizations of this technique. We then apply DPPs to the difficult problem of detecting and eliminating redundancy in fully-connected layers of neural networks. By placing a DPP over a layer, we are able to sample a subset of neurons that perform non-overlapping computations and merge all other neurons of the layer into the previous diverse subset. This allows us to significantly reduce the size of the neural network while simultaneously maintaining a good performance.
Kronecker Determinantal Point Processes
Determinantal Point Processes (DPPs) are probabilistic models over all subsets a ground set of N items. They have recently gained prominence in several applications that rely on “diverse” subsets. However, their applicability to large problems is still limited due to the O(N^3) complexity of core tasks such as sampling and learning. We enable efficient sampling and learning for DPPs by introducing KronDPP, a DPP model whose kernel matrix decomposes as a tensor product of multiple smaller kernel matrices. This decomposition immediately enables fast exact sampling. But contrary to what one may expect, leveraging the Kronecker product structure for speeding up DPP learning turns out to be more difficult. We overcome this challenge, and derive batch and stochastic optimization algorithms for efficiently learning the parameters of a KronDPP.
Diversity Networks: Neural Network Compression Using Determinantal Point Processes
We introduce Divnet, a flexible technique for learning networks with diverse neurons. Divnet models neuronal diversity by placing a Determinantal Point Process (DPP) over neurons in a given layer. It uses this DPP to select a subset of diverse neurons and subsequently fuses the redundant neurons into the selected ones. Compared with previous approaches, Divnet offers a more principled, flexible technique for capturing neuronal diversity and thus implicitly enforcing regularization. This enables effective auto-tuning of network architecture and leads to smaller network sizes without hurting performance. Moreover, through its focus on diversity and neuron fusing, Divnet remains compatible with other procedures that seek to reduce memory footprints of networks. We present experimental results to corroborate our claims: for pruning neural networks, Divnet is seen to be notably superior to competing approaches.
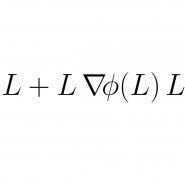
Fixed-point algorithms for learning determinantal point processes
Determinantal point processes (DPPs) offer an elegant tool for encoding probabilities over subsets of a ground set. Discrete DPPs are parametrized by a positive semidefinite matrix (called the DPP kernel), and estimating this kernel is key to learning DPPs from observed data. We consider the task of learning the DPP kernel, and develop for it a surprisingly simple yet effective new algorithm. Our algorithm offers the following benefits over previous approaches: (a) it is much simpler; (b) it yields equally good and sometimes even better local maxima; and (c) it runs an order of magnitude faster on large problems. We present experimental results on both real and simulated data to illustrate the numerical performance of our technique.
