Deep-learning
Publication Types:
Sparse MoEs meet Efficient Ensembles
Machine learning models based on the aggregated outputs of submodels, either at the activation or prediction levels, lead to strong performance. We study the interplay of two popular classes of such models: ensembles of neural networks and sparse mixture of experts (sparse MoEs). First, we show that these two approaches have complementary features whose combination is beneficial. Then, we present partitioned batch ensembles, an efficient ensemble of sparse MoEs that takes the best of both classes of models. Extensive experiments on fine-tuned vision transformers demonstrate the accuracy, log-likelihood, few-shot learning, robustness, and uncertainty calibration improvements of our approach over several challenging baselines. Partitioned batch ensembles not only scale to models with up to 2.7B parameters, but also provide larger performance gains for larger models.
Plex: Towards Reliability using Pretrained Large Model Extensions
A recent trend in artificial intelligence is the use of pretrained models for language and vision tasks, which have achieved extraordinary performance but also puzzling failures. Probing these models’ abilities in diverse ways is therefore critical to the field. In this paper, we explore the reliability of models, where we define a reliable model as one that not only achieves strong predictive performance but also performs well consistently over many decision-making tasks involving uncertainty (e.g., selective prediction, open set recognition), robust generalization (e.g., accuracy and proper scoring rules such as log-likelihood on in- and out-of-distribution datasets), and adaptation (e.g., active learning, few-shot uncertainty). We devise 10 types of tasks over 40 datasets in order to evaluate different aspects of reliability on both vision and language domains. To improve reliability, we developed ViT-Plex and T5-Plex, pretrained large model extensions for vision and language modalities, respectively. Plex greatly improves the state-of-the-art across reliability tasks, and simplifies the traditional protocol as it improves the out-of-the-box performance and does not require designing scores or tuning the model for each task. We demonstrate scaling effects over model sizes up to 1B parameters and pretraining dataset sizes up to 4B examples. We also demonstrate Plex’s capabilities on challenging tasks including zero-shot open set recognition, active learning, and uncertainty in conversational language understanding.
Ensembles of Classifiers: a Bias-Variance Perspective
Ensembles are a straightforward, remarkably effective method for improving the accuracy, calibration, and robustness of neural networks on classification tasks. Yet, the reasons underlying their success remain an active area of research. Building upon (Pfau, 2013), we turn to the bias-variance decomposition of Bregman divergences in order to gain insight into the behavior of ensembles under classification losses. Introducing a dual reparameterization of the bias-variance decomposition, we first derive generalized laws of total expectation and variance, then discuss how bias and variance terms can be estimated empirically. Next, we show that the dual reparameterization naturally introduces a way of constructing ensembles which reduces the variance and leaves the bias unchanged. Conversely, we show that ensembles that directly average model outputs can arbitrarily increase or decrease the bias. Empirically, we see that such ensembles of neural networks may reduce the bias. We conclude with an empirical analysis of ensembles over neural network architecture hyperparameters, revealing that these techniques allow for more efficient bias reduction than standard ensembles.
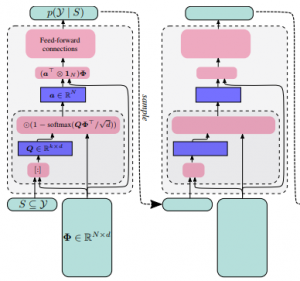
DppNet: Approximating Determinantal Point Processes with Deep Networks
Determinantal Point Processes (DPPs) provide an elegant and versatile way to sample sets of items that balance the point-wise quality with the set-wise diversity of selected items. For this reason, they have gained prominence in many machine learning applications that rely on subset selection. However, sampling from a DPP over a ground set of size N is a costly operation, requiring in general an O(N^3) preprocessing cost and an O(Nk^3) sampling cost for subsets of size k. We approach this problem by introducing DPPNets: generative deep models that produce DPP-like samples for arbitrary ground sets. We develop an inhibitive attention mechanism based on transformer networks that captures a notion of dissimilarity between feature vectors. We show theoretically that such an approximation is sensible as it maintains the guarantees of inhibition or dissimilarity that makes DPPs so powerful and unique. Empirically, we demonstrate that samples from our model receive high likelihood under the more expensive DPP alternative.

Learning and enforcing diversity with Determinantal Point Processes
As machine-learning techniques continue to require more data and become increasingly memory-heavy, being able to choose a subset of relevant, high-quality and diverse elements among large amounts of redundant or noisy data and parameters has become an important concern. Here, we approach this problem using Determinantal Point Processes (DPPs), probabilistic models that provide an intuitive and powerful way of balancing quality and diversity in sets of items. We introduce a novel, fixed-point algorithm for estimating the maximum likelihood parameters of a DPP, provide proof of convergence and discuss generalizations of this technique. We then apply DPPs to the difficult problem of detecting and eliminating redundancy in fully-connected layers of neural networks. By placing a DPP over a layer, we are able to sample a subset of neurons that perform non-overlapping computations and merge all other neurons of the layer into the previous diverse subset. This allows us to significantly reduce the size of the neural network while simultaneously maintaining a good performance.
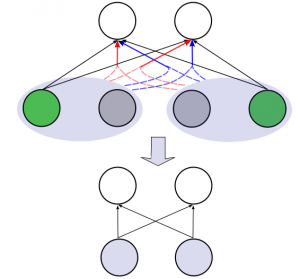
Diversity Networks: Neural Network Compression Using Determinantal Point Processes
We introduce Divnet, a flexible technique for learning networks with diverse neurons. Divnet models neuronal diversity by placing a Determinantal Point Process (DPP) over neurons in a given layer. It uses this DPP to select a subset of diverse neurons and subsequently fuses the redundant neurons into the selected ones. Compared with previous approaches, Divnet offers a more principled, flexible technique for capturing neuronal diversity and thus implicitly enforcing regularization. This enables effective auto-tuning of network architecture and leads to smaller network sizes without hurting performance. Moreover, through its focus on diversity and neuron fusing, Divnet remains compatible with other procedures that seek to reduce memory footprints of networks. We present experimental results to corroborate our claims: for pruning neural networks, Divnet is seen to be notably superior to competing approaches.
